Stacks and depth-first search
Contents
Introduction
As beautifully summarized by William Fiset ( LinkedIn) in his YouTube tutorial, a data structure is a object for organizing data so that it can be used (i.e., accessed / queried / updated). An abstract data type (ADT) is an abstraction of a data structure which provides only the interface to which a data structure must adhere to. The interface does not give any specific details about how something should be implemented or in what programming language.
There are a number of common ADTs, some listed in the table of abstractions below. This article will focus on defining the stack and demonstrating its utility in the implementation of the depth-first search algorithm.
| Abstraction | Implementation |
|---|---|
| vehicle | golf cart bicycle smart car |
| list | dynamic list linked list |
| queue | linked list based queue array based queue stack based queue |
| map | tree map hash map / hash table |
| stack | linked list |
Stacks
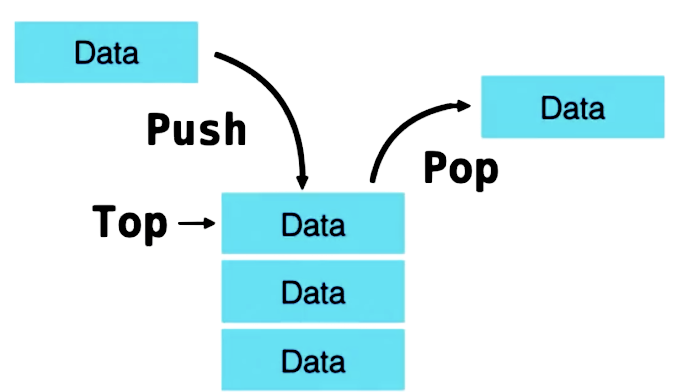
Credit: Modified from screenshot of William Fiset's YouTube tutorial.
A stack is a one-ended linear data structure which models a real world stack by having two primary operations: push and pop.
-
In its implementation there is a
toppointer to the data element at the top of the stack. - Items always get removed from or added to the top of the pile; this behavior is commonly called LIFO (last in first out).
In doing a (time) complexity analysis, we see that stacks perform really well! Constant time in nearly all operations except for search; search is linear in time because we may have to scan all elements in the stack.
| Operation | Complexity | Notes |
|---|---|---|
| pushing | O(1) | we have a pointer to the top element at all times |
| popping | O(1) | we have a pointer to the top element at all times |
|
peeking (returns the value at the top without removing it) |
O(1) | we have a pointer to the top element at all times |
| searching | O(n) | may need to scan all elements in the stack |
Stacks are used in a variety of contexts, including
- By undo mechanisms in text editors.
-
In compiler syntax checking for the matching brackets and braces.
The stack keeps track of the left brackets. When encountering a right bracket, the syntax checker- checks whether the stack is empty
-
peeks at the top element to see whether its equal to the reverse bracket - at the end of the script, checks that the stack is empty
- To model a pile of books or plates
- Behind the scenes to support recursion by keeping track of previous function calls
- To do a depth first search (DFS) on a graph
Depth-first search (DFS)
one of several graph traversal algorithms
As summarized by GeeksForGeeks, trees can be traversed in different ways: depth-first search (DFS) and breadth-first search (BFS, also known as level-order traversal). This is different from linear data structures (arrays, linked lists, queues, stacks), which only have one logical way to traverse them.
In comparing DFS to BFS, we see that DFS is better for path exploration while BFS is better for getting to more nodes faster. The table below provides a few additional points of comparison.
| depth-first search | breadth-first search |
|---|---|
| focused on exploring paths | focused on getting to more nodes faster |
| good for looking for paths, detecting cycles | good for any search that can be based on levels |
| associated with a stack data structure (LIFO) | associated with a queue data structure (FIFO) |
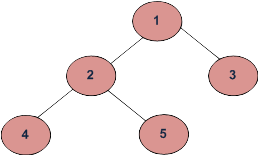
The DFS algorithm itself has several traversal types, explained below within the context of a tree example from GeeksForGeeks. The listing below gives the traversal method, the associated traversal order, and the result of that traversal on the example tree.
-
inorder (left, root, right): 4 2 5 1 3
-
traverse the left subtree, i.e., call
inorder(left_subtree) - visit the root
-
traverse the right subtree, i.e., call
inorder(right_subtree)
-
traverse the left subtree, i.e., call
-
preorder (root, left, right): 1 2 4 5 3
- visit the root
-
traverse the left subtree, i.e., call
preorder(left_subtree) -
traverse the right subtree, i.e., call
preorder(right_subtree)
-
postorder (left, root, right): 4 5 2 3 1
-
traverse the left subtree, i.e., call
postorder(left_subtree) -
traverse the right subtree, i.e., call
postorder(right_subtree) - visit the root
-
traverse the left subtree, i.e., call
It is most common to implement DFS recursively, as shown in the pseudocode below. The code assumes that the tree is structured as a linked list, and a tree node is of class TreeNode.
# to generate values from IG distribution
dfs(TreeNode current):
if current is null:
return false
if current satisfies condition:
return true
if current is leaf
return false
return dfs(current.left) or dfs(current.right)